
第一章 行列式:
1、行列式的定义:
(1)(仅)适用于2、3阶行列式的对角线法则;
(2)逆序数与排列的奇偶性;
(3)n阶行列式的定义(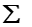 的意义与展开,展开式中项的规律与符号的确定(3种方式));
的意义与展开,展开式中项的规律与符号的确定(3种方式));
(4)抽象表示技能。
2、行列式的基本计算:
(1)利用定义计算;
(2)利用行列式的性质,化行列式为上(下)三角行列式计算;
(3)利用行列式的性质,化某行(列)只留一个(可能的)非零元,再用行列式的按行按列展开定理(子式,余子式,代数余子式)计算。
3、行列式的常用计算技巧:
(1)利用行和或列和相等的特点计算;
(2)加边法;
(3)同时拆行(列)法;
(4)递推法*;
(5)利用Vandermonde行列式计算;
(6) 数学归纳法*。
(此次考试仅要求有限阶的数字行列式与文字行列式的计算)
4、Cramer法则:
注意Cramer法则使用的前提条件:
(1)方程组的个数与未知量的个数相等;
(2)系数行列式不为零。
难点:抽象表示(n阶行列式的定义)、n阶行列式的计算。
第二章 矩阵及其运算
矩阵的各类运算:
- 乘法:
- 两矩阵相乘的前提(左矩阵的列数与右矩阵的行数相等);
- 乘法交换律不成立(导致乘法公式不成立,二项式公式不成立,消去律不成立);
- 积矩阵中元的表示。(
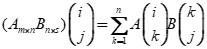 )
) - 转置、方阵的行列式、共轭矩阵:定义与运算性质(穿脱原理;
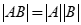 、
、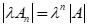 等)。
等)。 - 逆矩阵:
- 逆矩阵的定义;
- 可逆的充要条件(行列式不为零、非奇异、满秩);
- 伴随矩阵;利用伴随矩阵求逆。(注意伴随矩阵的计算程序,以保证计算结果的准确性)
- 矩阵的分块:
- 分块运算的定义,尤其是分块的转置、分块乘法中左(右)矩阵的块保持在左(右)边;
- 分块求逆法(设未知矩阵求解矩阵方程、准对角矩阵的求逆)
重点:矩阵的求逆(要求掌握各种求逆方法)。
第三章 矩阵的初等变换与线性方程组
1、矩阵的初等变换、行阶梯形矩阵、行最简矩阵;
2、子式、求矩阵的秩,三秩相等定理;
3、线性方程组的有解判别定理;
4、初等矩阵及八字原则(左行右列,首尾为主);
5、利用初等变换求矩阵的逆、求解矩阵方程。
第四章 向量组的线性相关性
1、线性表示、线性组合、两向量组的等价
2、 线性相关性:
- 定义(2个);
- 相关性的判别:转为向量方程是否有非零解,转为齐次线性方程组是否有非零解;转为求矩阵的秩;
向量组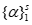 线性相关
线性相关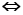 向量方程
向量方程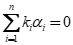 有非零解
有非零解
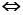 矩阵
矩阵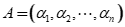 的秩
的秩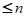
3、极大无关组、秩及其求法;(对矩阵施行初等行变换,不改变矩阵列向量之间的线性关系。)
4、相关性与矩阵间的关系(表示矩阵等);
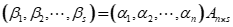
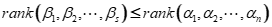 (即为基本定理)
(即为基本定理)- 当
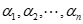 线性无关时,有
线性无关时,有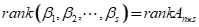
- 相关性的有关性质:
尤其是线性相性的基本定理:向量组A可由向量组B线性表示,
则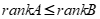 (
(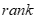 -秩)
-秩)
- 向量空间:
- 定义与判别;
- 生成子空间及相关性质:
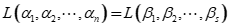
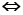
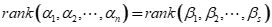
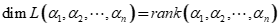
- 基与维数:能找出给定空间的基(一般为常见空间)
7、求解线性方程组(基础解系、通解、特解。有解判定定理。系数矩阵的秩与基础解系所含向量个数的关系)(注意求解程序,以保证计算的正确性)
基本题型:
- 相关性的证明;
- 求给定向量组的极大无关组、秩,并用该极大无关组表示其余向量;
- 相关性的判断;
- 求解线性方程组。
- 重点:线性相关性、求解线性方程组。
第五章 相似矩阵与二次型
1、向量的内积:定义(对称性、线性性、非负性)、长度、正交;
2、正交向量组、规范正交基、Schmidt正交化、正交矩阵、正交变换;
3、特征值、特征向量、特征多项式及Hamilton-Cayley定理、属于不同特征值的特征向量线性无关;
4、相似矩阵:定义(是矩阵间的一种等价关系)、相似矩阵具有相同的特征多项式、相似对角化、矩阵能相似对角化的充要条件、充分条件;
5、实对称矩阵的相似性:特征值必为实数、属于不同特征值的特征向量必正交、任一特征值的代数重数等于其几何重数、实对称矩阵必可相似对角化、实对称矩阵必可正交对角化;
6、二次型:二次型矩阵、二次型的秩、矩阵的合同变换、标准形、惯性定理;
7、二次型的正定性:正定二次型、正定矩阵、正定的充要条件、霍尔维茨定理(顺序主子式)。
基本题型:
1、 用正交变换化二次型为标准形;
2、 相似对角化及其证明;
3、 正定矩阵证明。
注意:注意有关结论的前提,是一般的方阵,还是实对称矩阵。
第六章 线性空间与线性变换
- 线性空间的定义:11条
- 线性空间的性质及证明:公理化方法
- 子空间的定义及其判断
- 维数、基与坐标:要求能熟练计算
- 线性空间的同构及应用同构理论解决一般线性空间中的问题
- 过渡矩阵与基变换、坐标变换:要求熟练矩阵表示,过渡矩阵的列向量的几何意义
- 线性变换与其在某基下矩阵:基下矩阵的列向量的几何意义
- 线性变换的性质与向量组与象向量组的线性关系:
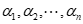 线性相关
线性相关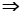
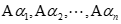 线性相关,但其逆不真。
线性相关,但其逆不真。
- 线性变换的象与核、线性变换的秩
- 同一线性变换在不同基下的矩阵相似。
基本题型:
- 线性空间与子空间的判定;
- 求给定间的基与维数、求给定向量在定间基下的坐标;
- 求过渡矩阵与基变换、坐标变换(常通过第三个基进行过渡)
- 求基下矩阵。
